|
ESCOLA:
E. E. PROF JOÃO PEDRO DO NASCIMENTO
|
|
DISCIPLINA: Matemática
|
SÉRIE: 8º ano - EF
|
|
PROFESSOR: Ana Maria
|
|
CONTEÚDO:
Notação Científica
|
HORAS/AULA:
06 aulas
|
|
DATA
DE ENVIO: 10/06/20
|
DATA
DE ENTREGA: 16/06/20
|
|
|
|
|
Objetivo da aula :
-Entender o que é
Notação Científica -Efetuar cálculos
com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação
científica
|
Nº
aulas
|
Nº
|
O QUE É PRA FAZER?
|
|
|
06
|
|
1- Ler com
muito atenção os textos de explicação
2-Assistir
os youtubes para complementar a aprendizagem
3-
Resolver as atividades propostas
OBS:
Tirar fotos e enviar para o WhatsApp
privado.
|
|
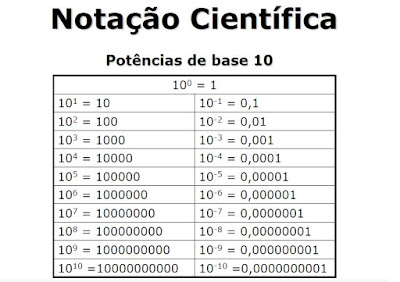
Notação científica- - O que é? Definição, como calcular e
características
A
notação científica é uma forma de
escrever números usando potência de 10. É utilizada para reduzir a escrita de
números que apresentam muitos algarismos. Números muito pequenos ou muito
grandes são frequentemente encontrados nas ciências em geral e escrever em notação científica facilita fazer
comparações e cálculos.
Primeiramente, se você parar para reparar, várias contas
matemáticas que realizamos na calculadora, por exemplo, não representam
números exatos.
Quase sempre vem aquele tanto de algarismos e você pensa, e agora? Pois bem, a
regra é que utilizemos sempre o primeiro
número significativo
mais os dois primeiros depois da vírgula. Certo? Pois bem, a essa técnica damos
o nome de notação científica.
Claro que isso foi apenas um exemplo simples. Em síntese, a
notação científica é utilizada por matemáticos, físicos,
astrônomos,
dentre outros profissionais, para tornar
números pequenos ou muito grandes de forma simplificada usando a
potência de base dez. Acima de tudo, a
fórmula para
tornar um número de acordo com a notação científica é
a·10n
Além disso, nesse sentido, a representa o que chamamos
de mantissa – também conhecido como coeficiente. Já o n representa o expoente ou ordem de grandeza dos números apresentados. Assim, para encontrar a
notação científica de um número, basta colocar a vírgula após o primeiro número
significante. Vamos entender melhor!
Notação científica na prática
Bom, se é dado um valor de
0,00045 e você precisa saber
qual a notação científica, o que fazer? Não se preocupe porque a técnica é
muito simples. Isso porque, o que queremos encontrar aqui é a mantissa desse valor, ou seja, o coeficiente. Assim, basta colocar a vírgula após o primeiro algarismo significativo seguindo da esquerda para
a direita, ou vice-versa. Nesse caso, o
coeficiente de 0,00045 será 4,5
Primeiramente, pode ocorrer exemplos como esse 3256565 em
que todos os números são significativos. Entretanto, a regra se aplica da mesma
maneira. Assim, o coeficiente do número 3256565 será 3,256565. Simples, não é?
Agora, vamos entender como a ordem de grandeza é
encontrada, que recebe esse nome porque determina qual a quantidade do número
na notação científica. Isso é muito comum, por exemplo, em
células atômicas
como
nêutrons, prótons e
elétrons que apresentam numerações
extensas. Mas como assim? Observe:
A massa do elétron, por exemplo, é representada pelo
número
0,000000000000000000000000000910938356
g. Logo, seria muito complexo realizar cálculos com essa quantidade de números,
não é? Para que se torne mais simplificado, a notação científica transforma esse
valor da seguinte maneira: 9,10938356·10– 28 g.
Nesse sentido, o coeficiente é 9,10938356 aplicando a potência de base dez.
Como encontrar a ordem de grandeza
Resumindo, para encontrar a ordem de grandeza é preciso se
atentar à uma questão muito importante. Vamos lá.
Pegando o exemplo anterior em que a notação científica da
massa do elétron é 9,10938356·10– 28 g
notamos que a ordem de grandeza, ou seja, o expoente, está negativo. Visto
isso, ao realocarmos a vírgula da massa do elétron andamos para a direta, sendo
representado no expoente como negativo.
Isso significa que, quando a vírgula for realocada para a
esquerda o expoente será positivo. Neste caso, por exemplo, o número 896000000000 possui coeficiente
8,96000000000. Sendo assim, o expoente da notação científica será positivo.
Dessa forma, observe o
expoente positivo e negativo nesses exemplos abaixo:
Aqui tem três explicações em youtubes pra você entender melhor A notação científica
na prática.
Notação científica com operações
Em síntese, sabemos que na matemática existe algumas formas
de cálculo, como a
soma, subtração, multiplicação e divisão.
Certo? Logo, para cada tipo de operação a notação científica será realizada de
uma forma .
.
Veja com atenção as explicações abaixo:
Para cada tipo de operação a notação científica será realizada de uma
forma.
Na multiplicação
Assim, na
multiplicação a conotação científica funciona multiplicado os números e, em
seguida, a base 10 é repetida e os expoentes são somados. Dessa forma, veja o
exemplo:
a) 1,4.10 3 x 3,1 . 10 2 = b) 2,5 . 10 – 8 x 2,3 . 10 6 =
(1,4 x 3,1) . 10 (3 + 2) = (2,5 x 2,3) . 10 ( – 8 + 6) =
4,34 . 10 5
5,75 .
10 – 2
Na divisão
Já na divisão ocorre
um pouco diferente. Sendo assim, em relação aos números devemos dividir,
repetir a base, e ao invés de somar os expoentes, na divisão devemos
subtraí-los. Visto isso, observe:
a) 9,42 .
10 5 : 1,2 . 10 2 = b) 8,64 . 10 – 3 : 3,2 . 10 6
=
(9,42 : 1,2) .
10 (5 – 2) = (8,64 : 3,2) . 10 ( – 3 – 6)
=
7,85 . 10 3 2,7
. 10 – 9
Na soma
e subtração
Por outro lado, na soma e subtração o próprio nome já diz. Nesse sentido,
os números são somados ou subtraídos e a potência 10 é repetida. Porém, para
que o cálculo seja realizado o expoente nas potências de 10 devem apresentar o
mesmo valor. Deste modo, veja:
a) 3,3 . 10 8 + 4,8 . 10 8 = b) 6,4 .
10 3 – 8,3 . 10 3
=
(3,3 + 4,8) . 10
8 =
(6,4 – 8,3) . 10 3 =
8,1 . 10 8 –
1,9 . 10 3
a) Atividades
1) Considere o
número 0,00000000000002, converta-o em notação científica.
2) O
número 349000 em notação científica corresponde a:
3) Escreva o
número 0,0004 em notação científica
4) Como
escrevemos 7,5 10-5 na
forma decimal?
5) Como
escrevemos 2,045 . 104 na forma decimal?
Seguindo os exemplos dado acima sobre
Notação científica com operações,resolva:
5) Faça a adição e subtração de 6,5 x 10³
e 2,3 x 10³
a) 6,5 x
10³ +
2,3 x 10³
b) 6,5 x
10³ -
2,3 x 10³
6) Realize a divisão e multiplicação
das notações científicas: de 5 x
10³ e 2,3 x 10²
a) 5 x 10³ X
2,3 x 10²
b) 5 x 10³ : 2,3 x 10²